抵抗を使った分圧の計算方法と、なぜそうなるか？を徹底解説

　電子回路の分圧の計算って、何も考えずにとりえず公式に当てはめていませんか？

　もちろん計算できればそれでいいかもしれませんが、どうしてそうなるのか？を深く理解しておけば、もし公式を忘れてしまっても自分で公式を導き出すことも可能です。

　本当かな？と思いますよね。本当です。今回に関してはキルヒホッフの法則、オームの法則、合成抵抗が理解できていれば暗記は不要です。なんでもかんでも暗記しなくても大丈夫です。

抵抗による分圧の公式の紹介

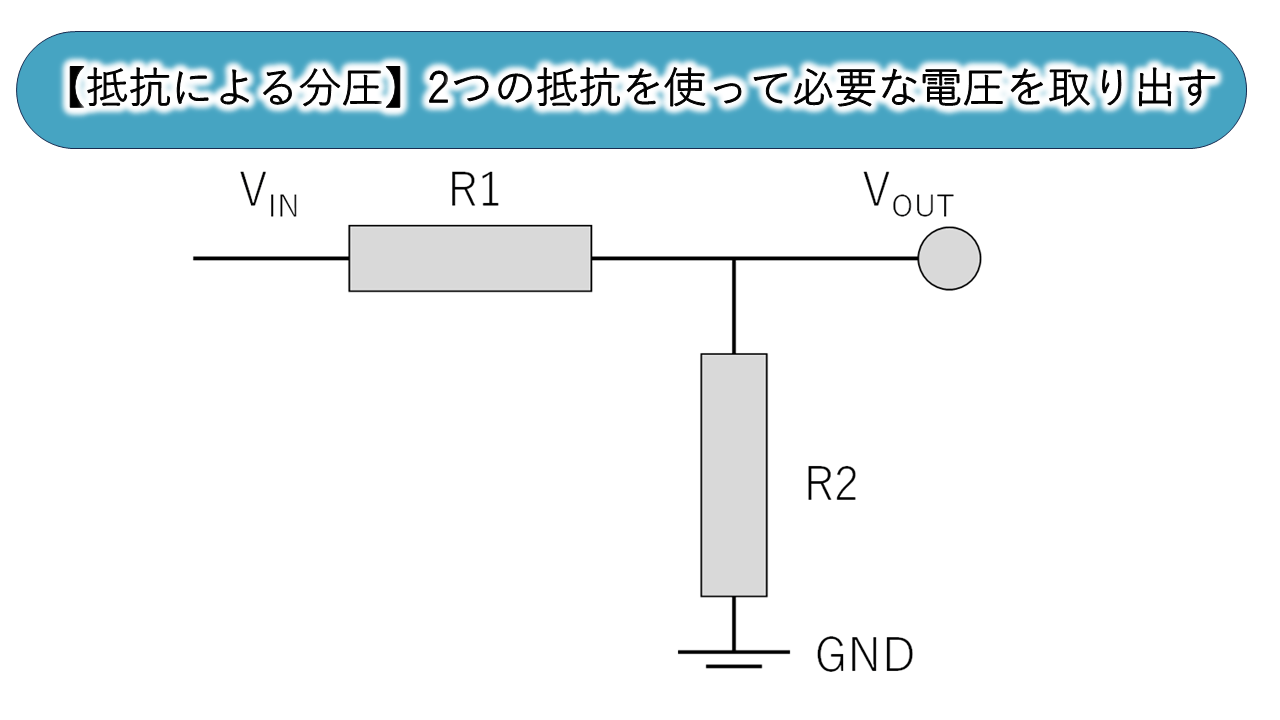
　まず、抵抗を複数使用して電圧を分ける、いわゆる分圧についてご紹介します。分圧は、電圧を分ける仕組みで、抵抗を2つ使うことで簡単に実現可能です。使用したい特定の電圧があったとして、高い電圧しか用意できない場合、狙った電圧まで落とすことが可能です。

　分圧回路に最低限必要な部品は、たった抵抗2つで済みます。必要な部品が少ないため手軽に使用できます。また、使用したい電圧を狙って計算ができることや、組み合わせもある程度好きに決められますので、自由度も高く使いやすい仕組みです。

分圧の公式

　そんな便利な分圧の計算方法をご紹介しておきましょう。
実例としては、

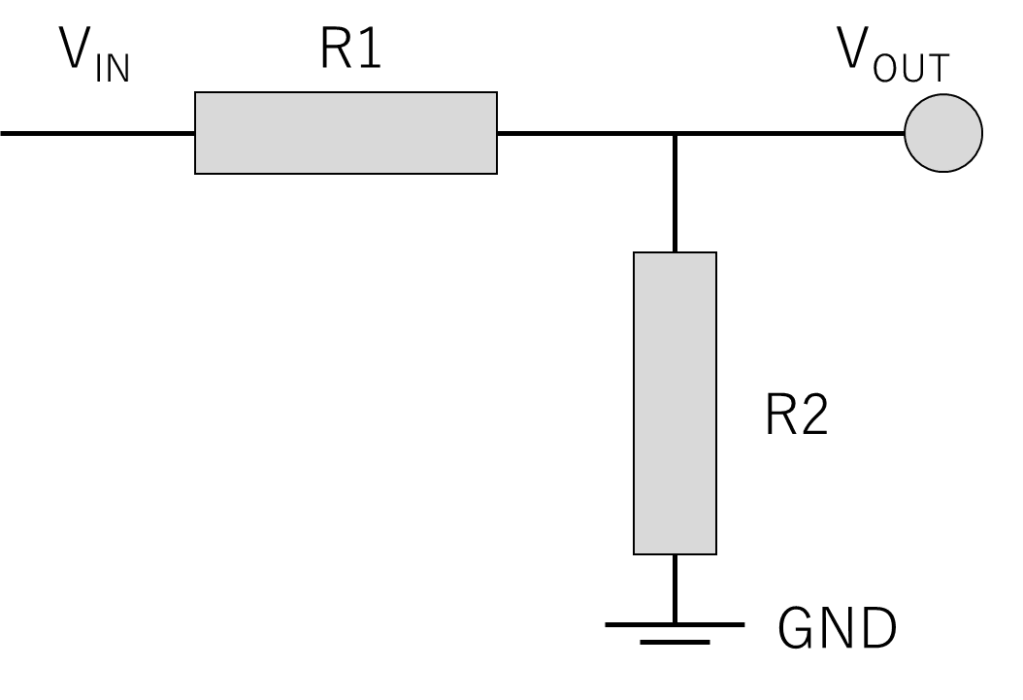
• 入力の電圧が\(V_{IN}\)
• 分圧後の電圧が\(V_{OUT}\)
• 分圧に使用した抵抗は\(R_1\)と\(R_2\)

としましょう。「分圧　公式」と調べればすぐに出てきますが、式としてはこうなります。

$$V_{OUT}=V_{IN} \times \dfrac {R_2}{R_1+R_2}$$

　この式を丸暗記する公式だと思っていませんか？当たり前ですが、この式を導出する方法はあります。しかも基本的な知識があれば、そんなに難しいテクニックは使いません。使うのはキルヒホッフの法則とオームの法則だけです。　

分圧に必要な、キルヒホッフの法則とは？

　分圧の計算でも登場するキルヒホッフの法則は、電流に関する「電流則」と「電圧則」があります。それぞれ、第一法則、第二法則と呼ばれます。どちらかというと、こちらの呼び方のほうがメジャーかもしれません。

　分圧では、第一法則と第二法則を組み合わせて使います。

キルヒホッフ第一法則「電流則」とは？

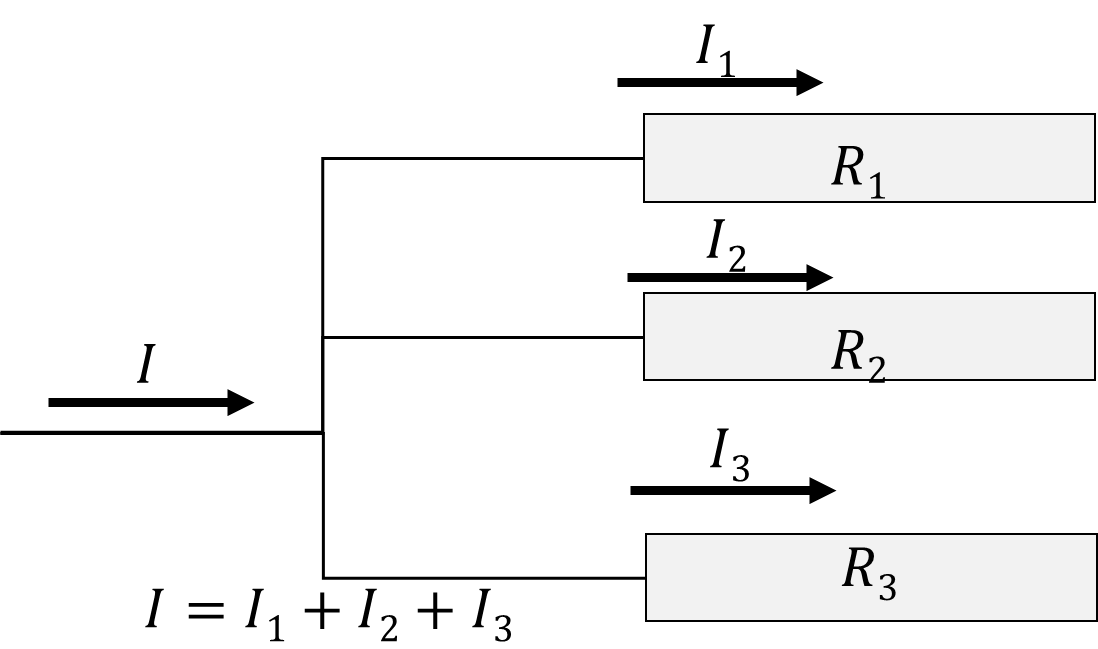
　キルヒホッフの第一法則である、電流則とは、回路の任意の点に注目したとき、流れ込む電流の総和と流れ出る電流の総和が常に等しいという法則です。つまり、回路のある点に10本でも20本でも抵抗を並列に追加して分岐したとしても、流れ出る電流の総和は、入力された電流と一致します。

キルヒホッフ第二法則「電圧則」とは？

　キルヒホッフの第二法則の電圧則は、その名の通り、電圧に関する法則です。法則の内容は、閉じた回路を見た時に、電源のような電圧を上げる部品と、抵抗のような電圧を下げる部品を合わせて全体として電圧が0になる法則です。ちょっと言葉だけだとわかりにくいですよね。

　例えばこんな回路があったとします。

　回路は、電源\(V\)と、抵抗が2つ\(R_1\)と\(R_2\)から成り立っています。\(R_1\)と\(R_2\)にかかる電圧を、それぞれ\(V_1\)と\(V_2\)とした場合には、次の式が成り立ちます。

$$V=V_1+V_2$$

　この式は、

$$V-V_1-V_2=0$$

　とも表現できます。これなら、回路の電圧の総和が0という法則とピッタリ一致しますね。電源の\(+V\)で電圧が上がり、その上がった電圧を抵抗の\(-V_1\)と\(-V_2\)で消費するイメージだとわかりやすいでしょうか。

具体的な回路例を使って分圧した電圧を計算する

　ここまで前提知識として、キルヒホッフの法則についてご紹介しました。ここからは、具体的に分圧の計算の仕組みについてご紹介します。分圧の計算は3Stepです。この3つだけ理解できれば丸暗記する必要はありません。それがこちらです。

　それでは順番にご紹介していきましょう。

合成抵抗を計算する。

　まずは、複数の抵抗を1つにまとめましょう。この場合だと、\(R_1\)と\(R_2\)の2つの抵抗が直列につながっています。直列の抵抗は足し算をすればいいので、合成抵抗\(R\)は\(R_1+R_2\)となります。

オームの法則を使って、抵抗に流れる電流値を計算する。

　合成抵抗\(R\)が\(R\)=\(R_1+R_2\)となるため、回路はこのように書き換えることができます。電源\(V\)と、抵抗\(R\)があるシンプルな回路です。

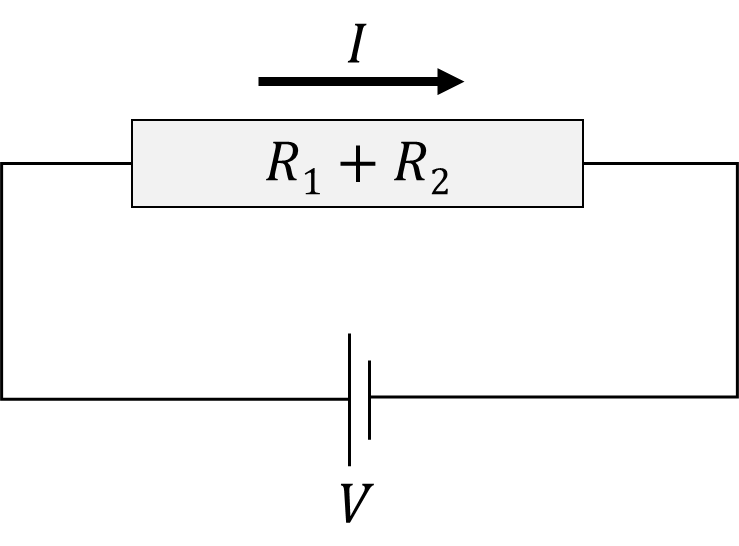
　この回路に流れる電流値を計算してみましょう。使うのはオームの法則です。オームの法則は覚えていますか？\(V=R\times\, I\)でしたね。自信が無い場合は、以前オームの法則を解説したこの記事をご覧ください。

　オームの法則がわかれば、この回路の全体に流れる電流値\(I\)は計算できますね。計算式はこうなります。

$$I=\frac{V}{R}$$

　\(R\)は合成抵抗で、\(R\)=\(R_1+R_2\)でしたから、計算式に代入すると、こうなります。

$$I=\frac{V}{R_1+R_2}$$

　これで合成抵抗に流れる電流値が計算できました。

キルヒホッフの法則を使って取り出す電圧を計算する。

　回路に流れる電流値は先ほどオームの法則により求まりました。残る作業は、2つの抵抗それぞれにどれくらいの電圧がかかっているか計算するだけです。

　直列の回路の場合、電流は分岐せずにスタートから最後まで一定で流れます。つまり、\(R_1\)と\(R_2\)どちらも同じ電流値が流れます。合成抵抗で足し算をして1つの抵抗とできたのも、分岐せず電流が他のところに洩れないからです。

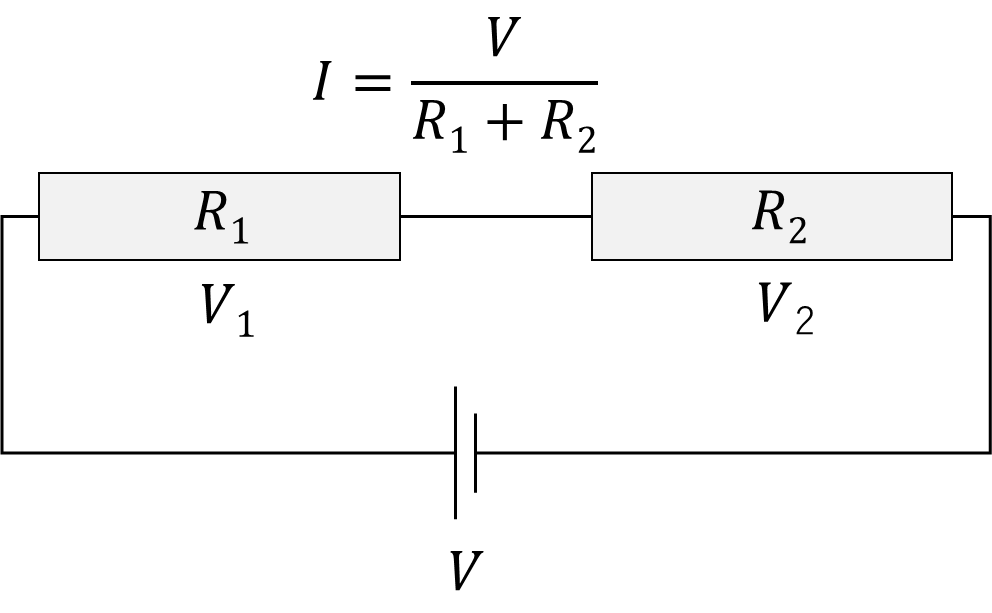
　具体的に\(R_1\)と\(R_2\)にかかる電圧をそれぞれ\(V_1\)と\(V_2\)として計算するとこうなります。

$$V_1=R_1\times I=\frac{R_1}{R_1+R_2}\times V$$

$$V_2=R_2\times I=\frac{R_2}{R_1+R_2}\times V$$

　この場合、\(R_1\)と\(R_2\)の間の点から分岐させて電圧を測定すると、\(R_2\)にかかる電圧を測定しているのと同じことになります。つまり\(V_{OUT}=V_2\)となります。

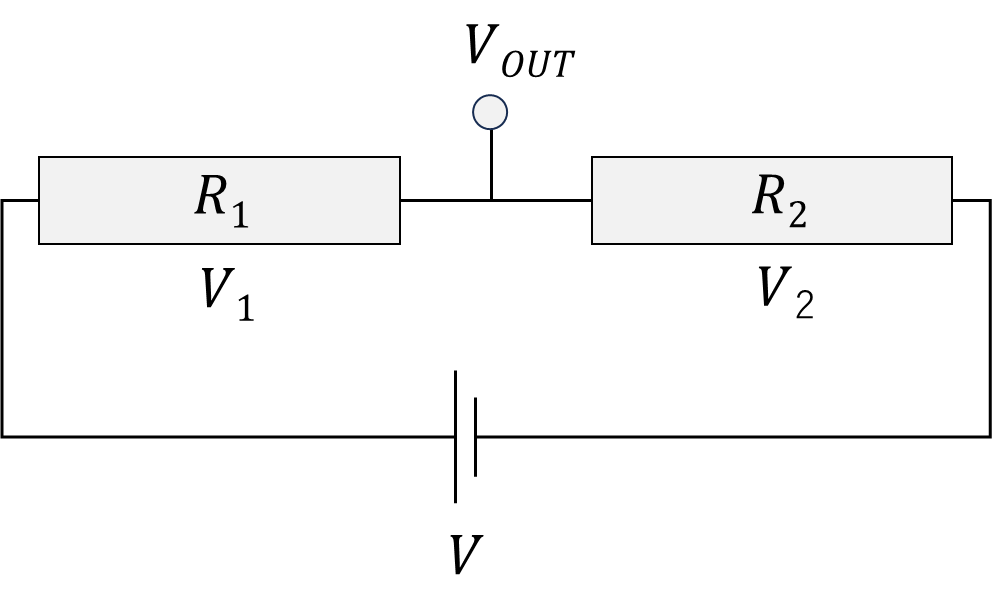
　最初の分圧の図に戻ってみましょう。どうでしょうか？

　この\(V_{OUT}\)って、実は\(R_2\)にかかっている電圧を取り出して利用するのと同じことなんですね。つまり一見回路の形が違うように見えますが、各抵抗値と電源の電圧を一致させれば、登場するVoutは値が一致します。これがわかると分圧の仕組みがより深く理解できると思います。

実際の数値を使って分圧した電圧を計算する

　文字式でここまでご紹介してきましたが、実務的には数値を扱うはずです。というわけで、各部品の特性値を設定して分圧した場合の電圧の計算をしてみましょう。回路はここまでなんども登場したこちらを使います。

計算に使う回路のパラメータ

　計算に使うパラメータは次のようにしてみましょう。

• \(V_{IN}:5V\)
• \(R_1:10k\omega\)
• \(R_2:15k\omega\)

分圧の計算

　先ほど決めたパラメータに従って計算してみましょう。分圧の式は次のように計算できました。おさらいです。

合成抵抗を計算する。

　まずは2つの抵抗の合計である、合成抵抗を求めましょう。

　\(R_1\)は\(10k \Omega\)で、\(R_2\)は\(15k \Omega\)ですから、合計は\(25k \Omega\)となります。これが合成抵抗の値です。

オームの法則を使って、抵抗に流れる電流値を計算する。

　次にオームの法則より、回路全体に流れる電流を計算しましょう。あらかじめ抵抗は合成して1つにまとめていますから、回路としては次のように表現できます。

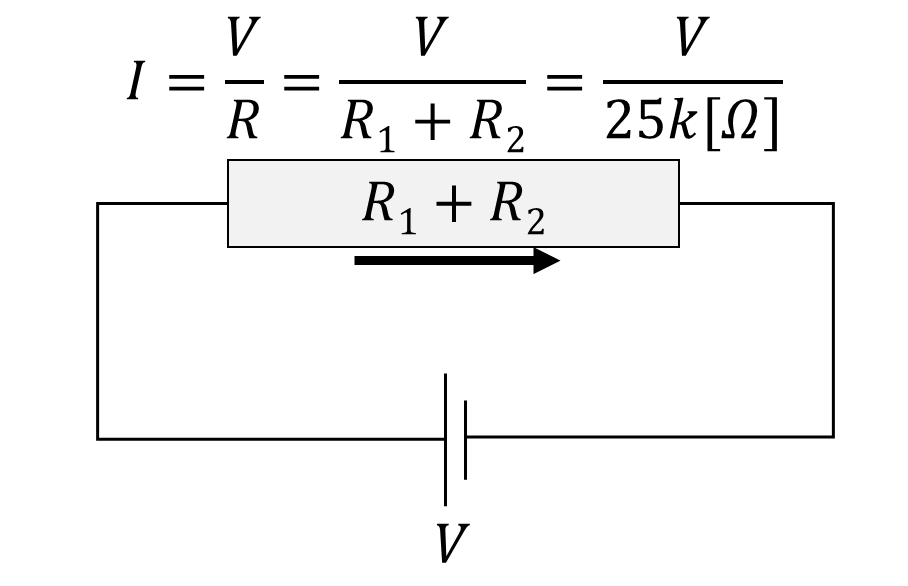
$$I=\dfrac {V}{25k\Omega}$$

となり、\(V\)=5Vですから、電流値\(I\)を具体的に求めると次のようになります。

$$I=\dfrac{5}{25k}=0.2[mA]$$

　つまり、抵抗に流れる電流値は、\(0.2mA\)であるとわかりました。

キルヒホッフの法則を使って取り出す電圧を計算する。

　最後にキルヒホッフの法則を使って、取り出す電圧を計算しましょう。取り出すのは、\(R_1\)と\(R_2\)の間です。図で表すと、\(V_{OUT}\)です。

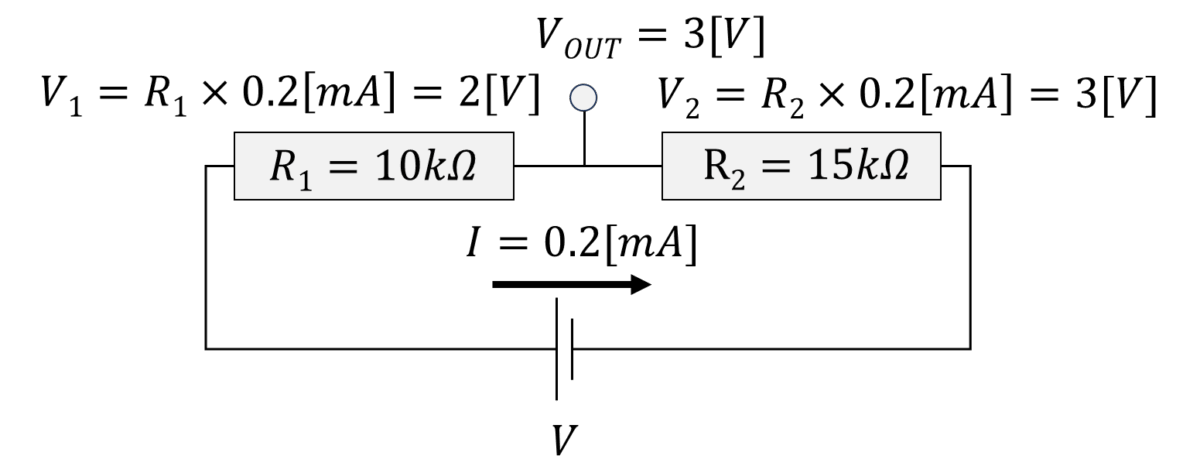
　\(V_{OUT}\)の位置は、抵抗の\(R_2\)にかかっている電圧を測定しているのと同じことになります。ですから、取り出す\(V_{OUT}\)は3\([V]\)となります。

　この結果からわかる通り、\(V_{OUT}\)を計算で一発で出すためには、$$V_{OUT}=V_{IN} \times \dfrac {R_2}{R_1+R_2}$$この式に当てはまることがわかりますね。

　

2個より多い抵抗を使って分圧する場合はどうか？

　ここまでは話を簡単にするために2個の抵抗を使って説明してきました。それでは、3個以上の抵抗を使った分圧の場合はどうなるでしょうか？実はここまでの話が理解できていれば、簡単に計算できます。

3個の抵抗を使う場合の分圧の式

　3個の抵抗を使う場合の分圧の式の求め方も、2つの抵抗の分圧の求め方と同じです。例えば、パラメータと回路が次のようになっていたとしましょう。

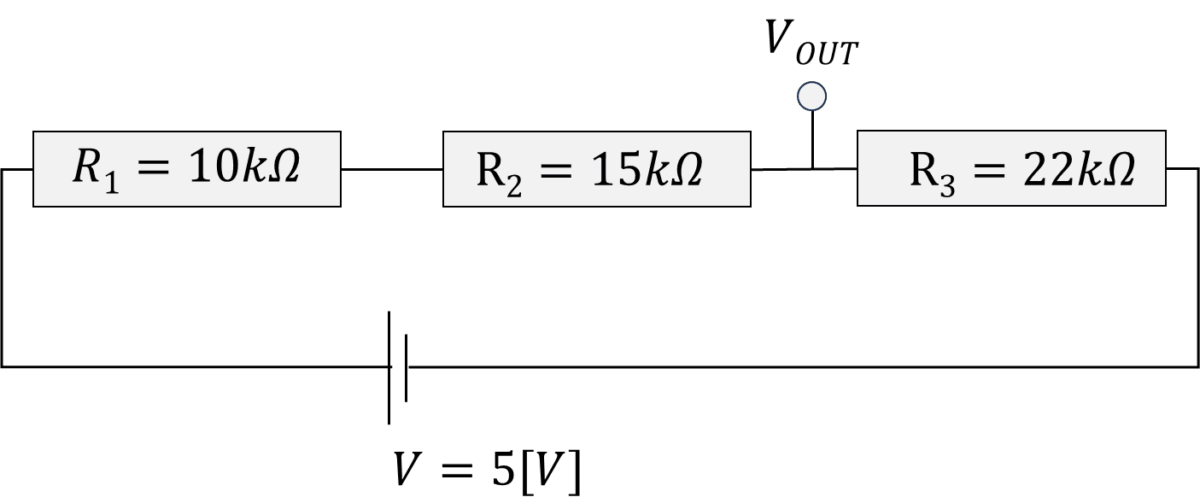
　この場合の合成抵抗\(R\)は、

$$R=10k+15k+22k=47k[\Omega]$$となります。

　次に回路全体を流れる電流値は、オームの法則より、\(I=\dfrac{5}{47k}=0.106[mA]\)となります。

　最後に、\(V_{OUT}\)にかかる電圧は、\(R_3\)にかかる電圧と等しいので、計算すると、\(V_{OUT}=22k\times0.106[mA]=2.33[V]\)となり、分圧することで\(2.33V\)が得られることがわかりました。

本当に分圧の計算通りになるの？実物で確認してみる。

　ここまでは計算上の話なので、この計算が実際に正しいのか？について実物で確認してみましょう。使うのは、5Vの電源が取れるArduinoと、\(10k\Omega\)と\(15k\Omega\)の抵抗が1つずつです。

　配線はここまで紹介してきた回路とまったく同じです。この状態で、3Vとテスタで表示されれば計算通りになっていると言えますね。

実際の様子

　実際の様子がこちらです。すでにArduinoの電源を入れているので、5Vが回路にかかっている状態です。

　\(15k\Omega\)にかかっている電圧を測定してみました。2.81Vなので、ほぼ3Vになっています。この結果より、計算と実物は大体一致することがわかると思います。

今回のまとめ：分圧の計算は仕組みを理解すれば暗記不要

　今回は分圧の計算について詳しく解説してみました。分圧というと、どうしても暗記が必要と思われがちですが、実際には、合成抵抗、キルヒホッフの法則、オームの法則という基本的な考え方だけで説明できます。

　ペーパーテストのように、計算に時間がかけられないような状況は公式として扱うのはアリですが、物事の原理を知るという意味でも今回のような式の導出もたまには刺激になって、いいのではないでしょうか？